calculo de volúmenes mediante secciones transversales.

 Para poder sacar una área  de una figura formada al pasar  dos ejes en diferentes puntos, se tiene que saber como primero que figura se esta trazando y en que puntos de limitación tiene.


Las secciones transversales más conocidas son cuadrado, rectángulo, triángulo, semicirculo y trapecio.

Para secciones transversales de área    A(x)    perpendiculares al eje    OX :
Si el área de la sección de un sólido situado entre los planos verticales     x = a    y    x = b    en el plano perpendícular al eje    OX  ,   en el punto de abscisa    x  ,   viene dada por la función continua    A(x)  ,   entonces, el volumen del sólido es:

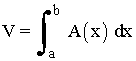
Para secciones transversales de área    A(y)    perpendiculares al eje    OY:
Si el área de la sección de un sólido situado entre los planos horizontales     y = c    y    y = d    en el plano perpendícular al eje    OY  ,   en el punto de ordenada   y  ,   viene dada por la función continua    A(y)  ,   entonces, el volumen del sólido es:

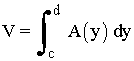
Un tema que nos va estar ayudando para poder tener en cuenta son las formulas de figuras para obtener una área

a continuación se deja para su apoyo :

calculo de area de figuras geometricas



Se dejara este video para ayuda de ejemplos de como calcular el área de una figura trazada en un plano 









 




El tema se ve complicado porque estamos incluyendo formulas establecidas para calcular una figura, una debilidad es tener que estar despejando ya sea un consiente a la indicación del problema, el desarrollo o solución del problema ya se pone mas sencillo por que   es el tema que estamos viendo.


Comentarios

Publicar un comentario

Entradas populares de este blog

solidos en revolucion

Imagen
  Físicamente, los sólidos de revolución se refieren todos aquellos objetos que son intersecados y se componen de una sección circular. Con el fin de entenderlos matemáticamente, sea f(x) una curva y sea esta rotada 360 grados alrededor del eje x entre el intervalo x = a y x = b. En la rotación, la curva representa un sólido y este sólido se denomina sólido de revolución. El cálculo del volumen de sólidos de revolución es una de las importantes aplicaciones de las integrales. El método integral del cálculo de volúmenes de sólidos de revolución se conoce comúnmente como Integración de Disco. solidos en revolucion Método de los discos  Para hallar el volumen de un sólido de revolución dividimos el sólido en rectángulos cuyo eje de revolución es el eje de x. La revolución de un rectángulo da lugar a un disco, por lo tanto este método divide al sólido en discos de ancho x , el ancho de cada rectángulo. Calculamos el área de cada disco ( región plana circular) con la fórmula de área de un c
Leer más

cambio de variables o por sustitución.

Imagen
para el cambio de una variable se tiene que derivar la función (x) para poder hacer la sustitución por las variables du/u, después se tiene que realizar la integración una vez teniendo esto solo se cambia valores con los resultados de du y de U.                                                        cambio de variables o por sustitución. se deja este video para una ayuda mas clara para la resolución del problema.   no es complicado los problemas, bueno asta ahorita pero es mucha solución para obtener el resultado. en lo personal vamos a buen ritmo en la enseñanza y esta clase de problemas nos ayudaran para unas futuras clases que tengamos en el transcurso del la carrera.
Leer más

calculo de maximos y minimos

Imagen
 el problema fundamental asociado al uso de las funciones para modelar problemas económicos consiste en calcular los valores de la variable independiente para los cuales la funcion toma un valor que se puede considerar maximo o minimo de la funcion la derivada de la funcion sub-ministra informacion en este sentido . es decir, una funcion es creciente si su grafica sube a medida de x y decrese, si su grafica baja amedida que x aumenta  se deja de un ejemplo de como sacar el minimo y maximo opinion: con tantas formulas poder encontrar la derivada te bloquea y no sabemos como iniciar.
Leer más