solidos en revolucion
Físicamente, los sólidos de revolución se refieren todos aquellos objetos que son intersecados y se componen de una sección circular.
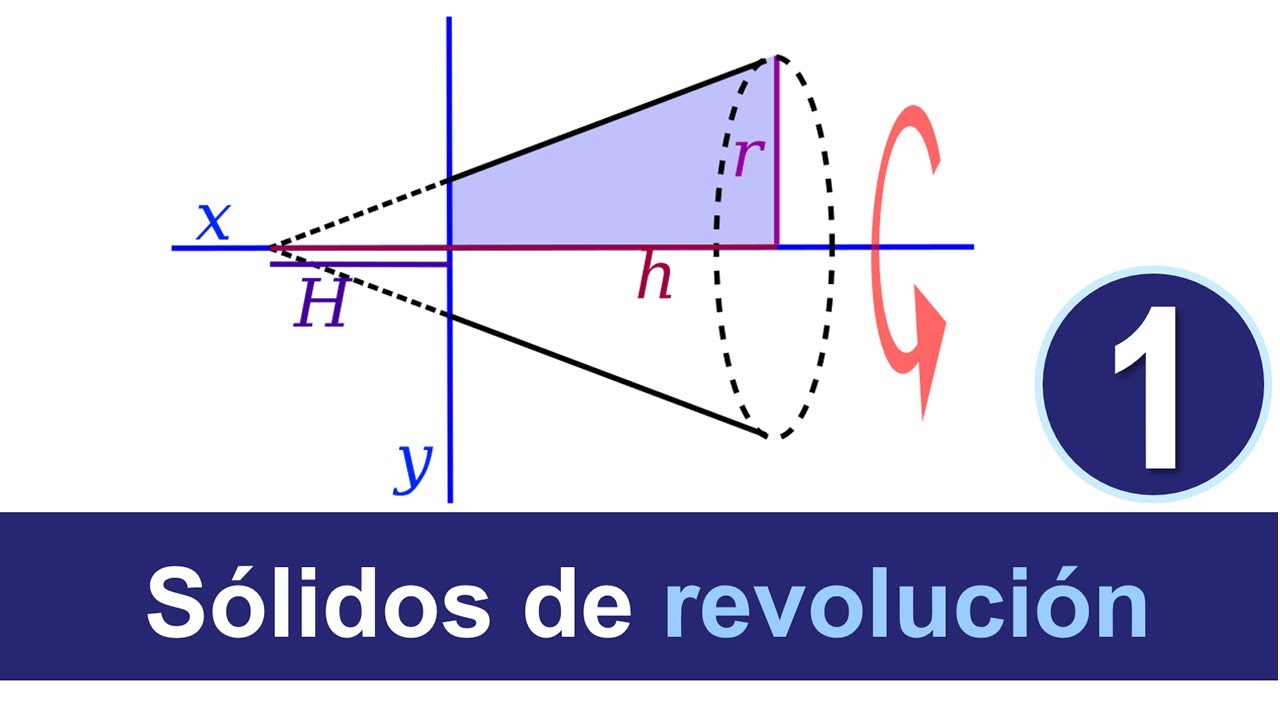
Con el fin de entenderlos matemáticamente, sea f(x) una curva y sea esta rotada 360 grados alrededor del eje x entre el intervalo x = a y x = b.
En la rotación, la curva representa un sólido y este sólido se denomina sólido de revolución.
El cálculo del volumen de sólidos de revolución es una de las importantes aplicaciones de las integrales.
El método integral del cálculo de volúmenes de sólidos de revolución se conoce comúnmente como Integración de Disco.
Método de los discos
Para hallar el volumen de un sólido de revolución dividimos el sólido en rectángulos cuyo eje de revolución es el eje de x. La revolución de un rectángulo da lugar a un disco, por lo tanto este método divide al sólido en discos de ancho x , el ancho de cada rectángulo. Calculamos el área de cada disco ( región plana circular) con la fórmula de área de un círculo. Para calcular el volumen multiplicamos el área de la región circular por el ancho del rectángulo ( x ) que lo forma.
Fórmula del volumen por disco
Método de Arandelas
El método de Arandelas o Washer, es una extensión del método de discos para sólidos huecos. Donde se tiene un radio interno r y un radio R externo de la arandela.  La integral que contiene el radio interno representa el volumen del hueco y se resta de la integral que contiene el radio externo.  |
Comentarios
Publicar un comentario